Mousai: An Open-Source General Purpose Harmonic Balance Solver¶
In [3]:
%matplotlib inline
%load_ext autoreload
%autoreload 2
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import mousai as ms
from scipy import pi, sin
matplotlib.rcParams['figure.figsize'] = (11, 5)
from traitlets.config.manager import BaseJSONConfigManager
path = "/Users/jslater/anaconda3/etc/jupyter/nbconfig"
cm = BaseJSONConfigManager(config_dir=path)
cm.update("livereveal", {
"theme": "sky",
"transition": "zoom",
})
The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload
Out[3]:
{'theme': 'sky', 'transition': 'zoom'}
Overview¶
A wide array of contemporary problems can be represented by nonlinear ordinary differential equations with solutions that can be represented by Fourier Series:
Limit cycle oscillation of wings/blades
Flapping motion of birds/insects/ornithopters
Flagellum (threadlike cellular structures that enable bacteria etc. to swim)
Shaft rotation, especially including rubbing or nonlinear bearing contacts
Engines
Radio/sonar/radar electronics
Wireless power transmission
Power converters
Boat/ship motions and interactions
Cardio systems (heart/arteries/veins)
Ultrasonic systems transversing nonlinear media
Responses of composite materials or materials with cracks
Near buckling behavior of vibrating columns
Nonlinearities in power systems
Energy harvesting systems
Wind turbines
Radio Frequency Integrated Circuits
Any system with nonlinear coatings/friction damping, air damping, etc.
These can all be observed in a quick literature search on ‘Harmonic Balance’.
Why (did I) write Mousai?¶
The ability to code harmonic balance seems to be publishable by itself
It’s not research- it’s just application of a known family of technique
A limited number of people have this knowledge and skill
Most cannot access this technique
“Research effort” is spent coding the technique, not doing research
Why write Mousai? (continued)¶
Matlab command eig unleashed power to the masses
Very few papers are published on eigensolutions- they have to be better than
eigeigonly provides simple access to high-end eigensolvers written inCandFortranUndergraduates with no practical understanding of the algorithms easily solve problems that were intractable a few decades ago.
Access and ease of use of such techniques enable greater science and greater research.
The real world is nonlinear, but linear analysis dominates because the tools are easier to use.
With
Mousai, an undergraduate can solve a nonlinear harmonic response problem easier then a PhD can today.
Theory:¶
Linear Solution¶
Most dynamics systems can be modeled as a first order differential equation
- Use finite differences
- Use Galerkin methods (Finite Elements)
- Of course- discrete objects
This is the common State-Space form: -solutions exceedingly well known if it is linear
Finding the oscillatory response, after dissipation of the transient response, requires long time marching.
Without damping, this may not even been feasible.
With damping, tens, hundreds, or thousands of cycles, therefore thousands of times steps at minimum.
For a linear system in the frequency domain this is
where
are constant matrices.
The solution is:
where the magnitudes and phases of the elements of \(\mathbf{Z}\) provide the amplitudes and phases of the harmonic response of each state at the frequency \(\omega\).
Nonlinear solution¶
For a nonlinear system in the frequency domain we assume a Fourier series solution
\(N=1\) for a single harmonic. \(n=0\) is the constant term.
This can be substituted into the governing equation to find \(\dot{\mathbf{z}}(t)\):
This is actually a function call to a Finite Element Package, CFD, Matlab function, - whatever your solver uses to get derivatives
We can also find \(\dot{\mathbf{z}}(t)\) from the derivative of the Fourier Series:
The difference between these methods is zero when \(\mathbf{Z}_n\) are correct.
These operations are wrapped inside a function that returns this error
This function is used by a Newton-Krylov nonlinear algebraic solver.
Calls any solver in the SciPy family of solvers with the ability to easily pass through parameters to the solver and to the external derivative evaluator.
Examples:¶
Duffing Oscillator¶
In [4]:
# Define our function (Python)
def duff_osc_ss(x, params):
omega = params['omega']
t = params['cur_time']
xd = np.array([[x[1]],
[-x[0] - 0.1 * x[0]**3 - 0.1 * x[1] + 1 * sin(omega * t)]])
return xd
In [5]:
# Arguments are name of derivative function, number of states, driving frequency,
# form of the equation, and number of harmonics
t, x, e, amps, phases = ms.hb_time(duff_osc_ss, num_variables=2, omega=.1,
eqform='first_order', num_harmonics=5)
print('Displacement amplitude is ', amps[0])
print('Velocity amplitude is ', amps[1])
Displacement amplitude is 0.9469563546008394
Velocity amplitude is 0.09469563544416415
Mousai can easily recreate the near-continuous response¶
time, xc = ms.time_history(t, x)
In [6]:
def pltcont():
time, xc = ms.time_history(t, x)
disp_plot, _ = plt.plot(time, xc.T[:, 0], t,
x.T[:, 0], '*b', label='Displacement')
vel_plot, _ = plt.plot(time, xc.T[:, 1], 'r',
t, x.T[:, 1], '*r', label='Velocity')
plt.legend(handles=[disp_plot, vel_plot])
plt.xlabel('Time (sec)')
plt.title('Response of Duffing Oscillator at 0.0159 rad/sec')
plt.ylabel('Response')
plt.legend
plt.grid(True)
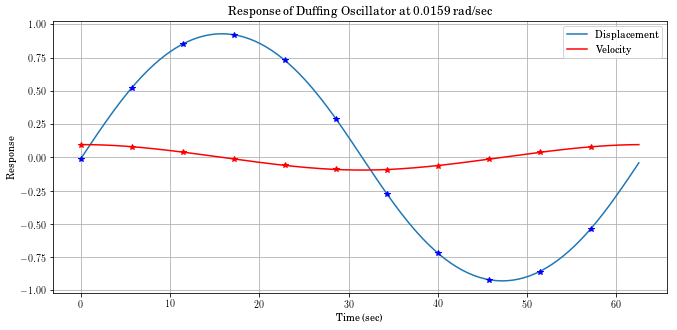
In [7]:
fig=plt.figure()
ax=fig.add_subplot(111)
time, xc = ms.time_history(t, x)
disp_plot, _ = ax.plot(time, xc.T[:, 0], t,
x.T[:, 0], '*b', label='Displacement')
vel_plot, _ = ax.plot(time, xc.T[:, 1], 'r',
t, x.T[:, 1], '*r', label='Velocity')
ax.legend(handles=[disp_plot, vel_plot])
ax.set_xlabel('Time (sec)')
ax.set_title('Response of Duffing Oscillator at 0.0159 rad/sec')
ax.set_ylabel('Response')
ax.legend
ax.grid(True)
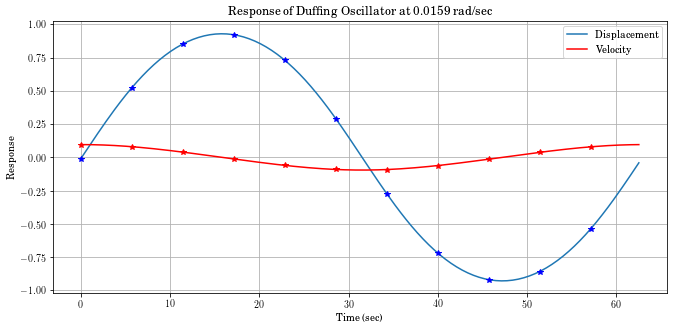
In [19]:
pltcont()# abbreviated plotting function
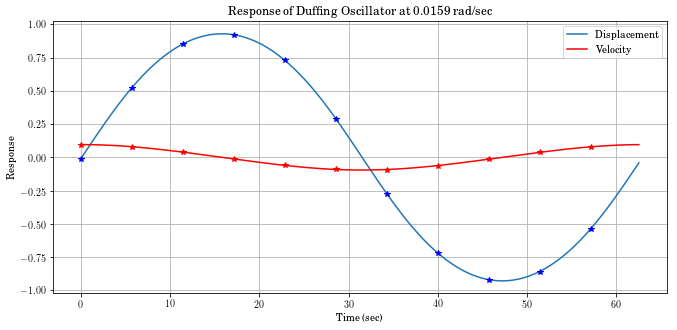
In [20]:
time, xc = ms.time_history(t, x)
disp_plot, _ = plt.plot(time, xc.T[:, 0], t,
x.T[:, 0], '*b', label='Displacement')
vel_plot, _ = plt.plot(time, xc.T[:, 1], 'r',
t, x.T[:, 1], '*r', label='Velocity')
plt.legend(handles=[disp_plot, vel_plot])
plt.xlabel('Time (sec)')
plt.title('Response of Duffing Oscillator at 0.0159 rad/sec')
plt.ylabel('Response')
plt.legend
plt.grid(True)
In [21]:
omega = np.arange(0, 3, 1 / 200) + 1 / 200
amp = sp.zeros_like(omega)
amp[:] = np.nan
t, x, e, amps, phases = ms.hb_time(duff_osc_ss, num_variables=2,
omega=1 / 200, eqform='first_order', num_harmonics=1)
for i, freq in enumerate(omega):
# Here we try to obtain solutions, but if they don't work,
# we ignore them by inserting `np.nan` values.
x = x - sp.average(x)
try:
t, x, e, amps, phases =
ms.hb_time(duff_osc_ss, x0=x,
omega=freq, eqform='first_order', num_harmonics=1)
amp[i] = amps[0]
except:
amp[i] = np.nan
if np.isnan(amp[i]):
break
plt.plot(omega, amp)
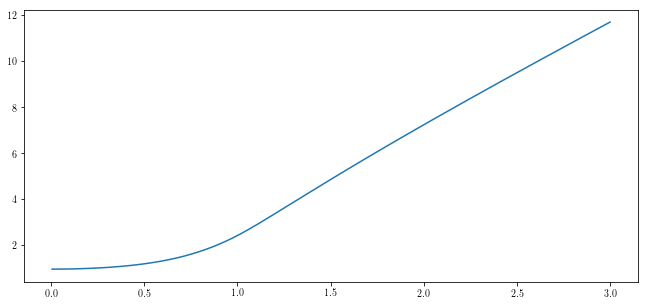
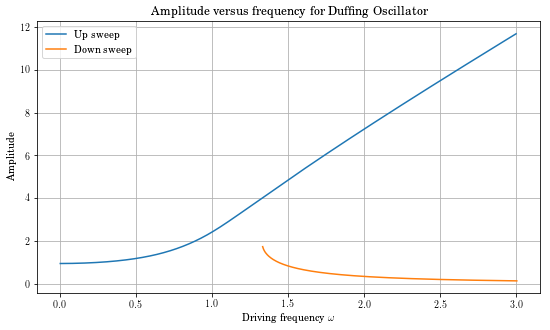
Let’s sweep through driving frequencies to find a frequency response function¶
In [10]:
omegal = np.arange(3, .03, -1 / 200) + 1 / 200
ampl = sp.zeros_like(omegal)
ampl[:] = np.nan
t, x, e, amps, phases = ms.hb_time(duff_osc_ss, num_variables=2,
omega=3, eqform='first_order', num_harmonics=1)
for i, freq in enumerate(omegal):
# Here we try to obtain solutions, but if they don't work,
# we ignore them by inserting `np.nan` values.
x = x - np.average(x)
try:
t, x, e, amps, phases = ms.hb_time(duff_osc_ss, x0=x,
omega=freq, eqform='first_order', num_harmonics=1)
ampl[i] = amps[0]
except:
ampl[i] = np.nan
if np.isnan(ampl[i]):
break
In [8]:
plt.plot(omega,amp, label='Up sweep')
plt.plot(omegal,ampl, label='Down sweep')
plt.legend()
plt.title('Amplitude versus frequency for Duffing Oscillator')
plt.xlabel('Driving frequency $\\omega$')
plt.ylabel('Amplitude')
plt.grid()
Two degree of freedom system¶
In [11]:
def two_dof_demo(x, params):
omega = params['omega']
t = params['cur_time']
force_amplitude = params['force_amplitude']
alpha = params['alpha']
# The following could call an external code to obtain the state derivatives
xd = np.array([[x[1]],
[-2 * x[0] - alpha * x[0]**3 + x[2]],
[x[3]],
[-2 * x[2] + x[0]]] + force_amplitude * np.sin(omega * t))
return xd
Let’s find a response.¶
In [12]:
parameters = {'force_amplitude': 0.2}
parameters['alpha'] = 0.4
t, x, e, amps, phases = ms.hb_time(two_dof_demo, num_variables=4,
omega=1.2, eqform='first_order', params=parameters)
amps
Out[12]:
array([0.86696762, 0.89484597, 0.99030411, 1.04097851])
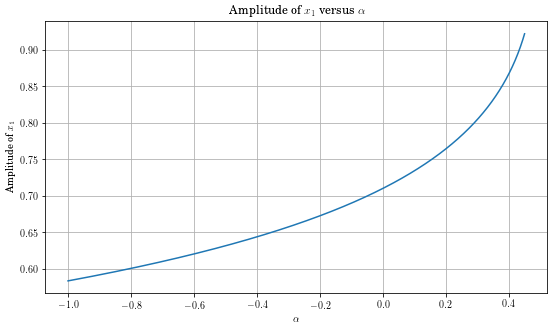
Or a parametric study of response amplitude versus nonlinearity.¶
In [13]:
alpha = np.linspace(-1, .45, 2000)
amp = np.zeros_like(alpha)
for i, alphai in enumerate(alpha):
parameters['alpha'] = alphai
t, x, e, amps, phases = ms.hb_time(two_dof_demo, num_variables=4, omega=1.2,
eqform='first_order', params=parameters)
amp[i] = amps[0]
In [12]:
plt.plot(alpha,amp)
plt.title('Amplitude of $x_1$ versus $\\alpha$')
plt.ylabel('Amplitude of $x_1$')
plt.xlabel('$\\alpha$')
plt.grid()
Two degree of freedom system with Coulomb Damping¶
In [16]:
def two_dof_coulomb(x, params):
omega = params['omega']
t = params['cur_time']
force_amplitude = params['force_amplitude']
mu = params['mu']
# The following could call an external code to obtain the state derivatives
xd = np.array([[x[1]],
[-2 * x[0] - mu * np.abs(x[1]) + x[2]],
[x[3]],
[-2 * x[2] + x[0]]] + force_amplitude * np.sin(omega * t))
return xd
In [17]:
parameters = {'force_amplitude': 0.2}
parameters['mu'] = 0.1
t, x, e, amps, phases = ms.hb_time(two_dof_coulomb, num_variables=4,
omega=1.2, eqform='first_order', params=parameters)
amps
Out[17]:
array([0.68916938, 0.68228248, 0.67299991, 0.66065019])
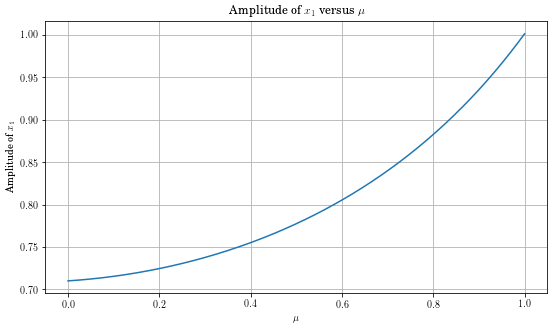
In [18]:
mu = np.linspace(0, 1.0, 200)
amp = np.zeros_like(mu)
for i, mui in enumerate(mu):
parameters['mu'] = mui
t, x, e, amps, phases = ms.hb_time(two_dof_coulomb, num_variables=4, omega=1.2,
eqform='first_order', num_harmonics=3, params=parameters)
amp[i] = amps[0]
Too much Coulomb friction can increase the response.¶
Did you know that?
This damping shifted resonance.
In [32]:
plt.plot(mu,amp)
plt.title('Amplitude of $x_1$ versus $\\mu$')
plt.ylabel('Amplitude of $x_1$')
plt.xlabel('$\\mu$')
plt.grid()
But can I solve an equation in one line? Yes!!!¶
Damped Duffing oscillator in one command.
In [25]:
out = ms.hb_time(lambda x, v,
params: np.array([[-x - .1 * x**3 - .1 * v + 1 *
sin(params['omega'] * params['cur_time'])]]),
num_variables=1, omega=.7, num_harmonics=1)
out[3][0]
Out[25]:
1.4779630014433971
OK - that’s a bit obtuse. I wouldn’t do that normally, but Mousai can.
How to get this?¶
Install Scientific Python from SciPy.org
AFRL: See your tech support to get the Enthought distribution installed
See the Mousai documents for installation instructions
pip install mousaiAFRL: Talk to me- install is easy if I send you the files.
See Mousai on GitHub (https://github.com/josephcslater/mousai)
Conclusions¶
Nonlinear frequency solutions are within reach of undergraduates
Installation is trivial
Already in use (GitHub logs indicate dozens of users)
Custom special case and proprietary solvers such as BDamper can be replaced for free
Research potential is about to be unleashed
Future¶
Add time-averaging method
currently requires high number of harmonics for non-smooth systems
Add masking of known harmonics (average is often fixed and known)
Automated sweep control
Branch following
Condense the one-line method
Evaluate on large scale problems
Currently attempting to hook to ANSYS
Parallelize
Leverage CUDA
In [ ]: