Duffing Oscillator Solution¶
In [1]:
%matplotlib inline
%load_ext autoreload
%autoreload 2
import scipy as sp
import numpy as np
import matplotlib.pyplot as plt
import mousai as ms
from scipy import pi, sin
In [3]:
# Test that all is working.
# f_tol adjusts accuracy. This is smaller than reasonable, but illustrative of usage.
t, x, e, amps, phases = ms.hb_time(ms.duff_osc, sp.array([[0,1,-1]]), .7, f_tol = 1e-12)
print('Equation errors (should be zero): ',e)
print('Constant term of FFT of signal should be zero: ', ms.fftp.fft(x)[0,0])
Equation errors (should be zero): [[ 1.11022302e-15 -1.68753900e-14 1.33226763e-15]]
Constant term of FFT of signal should be zero: (-0.10771053458129715+0j)
In [3]:
# Using more harmonics.
t, x, e, amps, phases = ms.hb_time(ms.duff_osc, x0 = sp.array([[0,1,-1]]), omega = .7, num_harmonics= 7)
print('Equation errors (should be zero): ', e)
print('Constant term of FFT of signal should be zero: ', ms.fftp.fft(x)[0,0])
Equation errors (should be zero): [[ 2.04616314e-08 -1.11916120e-08 -4.32641484e-09 -8.27785285e-10
-1.06717036e-08 -2.49418783e-07 -6.82304595e-07 -1.59994936e-07
-3.88299430e-11 9.85229565e-09 1.56362223e-09 -1.71778813e-10
7.32659703e-08 4.91827027e-07 5.65568172e-07]]
Constant term of FFT of signal should be zero: (7.04098108967e-06+0j)
Sometimes we can improve just by restarting from the prior end point. Sometimes, we just think it’s improved.
In [4]:
t, x, e, amps, phases = ms.hb_time(ms.duff_osc, x0 = x, omega = .7, num_harmonics= 7)
print('Errors: ', e)
print('Constant term of FFT of signal should be zero: ', ms.fftp.fft(x)[0,0])
Errors: [[ 7.29971639e-15 2.38697950e-15 1.02140518e-14 1.55431223e-14
2.88657986e-14 -4.44089210e-16 -1.30007116e-13 -1.18793864e-14
-5.61399885e-15 -1.65978342e-14 -2.33146835e-15 -1.99840144e-15
-2.56461519e-14 7.13873405e-14 1.18960397e-13]]
Constant term of FFT of signal should be zero: (7.08481329931e-06+0j)
/Users/jslater/anaconda3/lib/python3.6/site-packages/scipy/optimize/nonlin.py:474: RuntimeWarning: invalid value encountered in double_scalars
and dx_norm/self.x_rtol <= x_norm))
In [5]:
# Let's get a smoother response
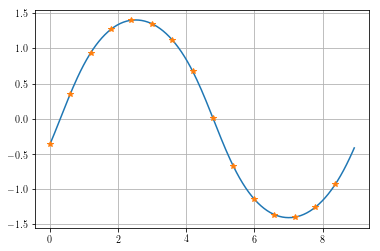
time, xc = ms.time_history(t,x)
plt.plot(time,xc.T,t,x.T,'*')
plt.grid(True)
print('The average for this problem is known to be zero, we got', sp.average(x))
The average for this problem is known to be zero, we got 4.72320886587e-07
In [26]:
def duff_osc2(x, v, params):
omega = params['omega']
t = params['cur_time']
return np.array([[-x-.1*x**3-.1*v+1*sin(omega*t)]])
In [27]:
t, x, e, amps, phases = ms.hb_time(duff_osc2, sp.array([[0,1,-1]]), .7, num_harmonics=5)
print(x,e)
print('Constant term of FFT of signal should be zero: ', ms.fftp.fft(x)[0,0])
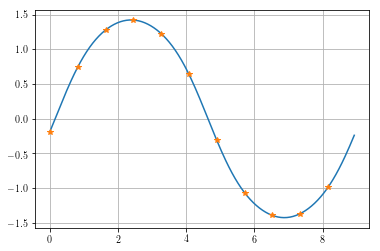
time, xc = ms.time_history(t,x)
plt.plot(time, xc.T, t, x.T, '*')
plt.grid(True)
[[-0.1854827 0.74408211 1.27869989 1.42305317 1.22766696 0.6400849
-0.31045409 -1.06650367 -1.39410353 -1.36873107 -0.98898229]] [[ 3.18347107e-09 -5.75875847e-10 -6.27391217e-09 -7.88667857e-08
-2.08381912e-07 -1.90325802e-08 1.15335749e-09 3.95564803e-10
2.19995009e-08 1.48110614e-07 1.50174076e-07]]
Constant term of FFT of signal should be zero: (-0.000670319513207+0j)
In [28]:
omega = sp.linspace(0.1,3,200)+1/200
amp = sp.zeros_like(omega)
x = sp.array([[0,-1,1,0,0]])
for i, freq in enumerate(omega):
#print(i,freq,x)
try:
t, x, e, amps, phases = ms.hb_time(duff_osc2, x, freq)#, f_tol = 1e-10)#, callback = resid)
amp[i]=amps[0]
except:
amp[i] = sp.nan
plt.plot(omega, amp)
Out[28]:
[<matplotlib.lines.Line2D at 0x10d892a20>]
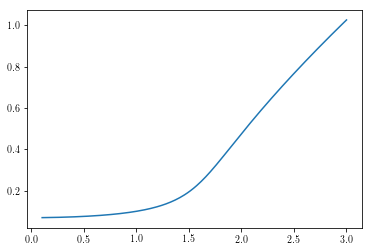
The break is an indicative of a break in the branch and is actually a
result of the solution being unstable. Not the system, but the
solution. By that we mean that while this is considered a solution, it
isn’t one that will actually continue in a real situation and another
solution will necessarily be found.
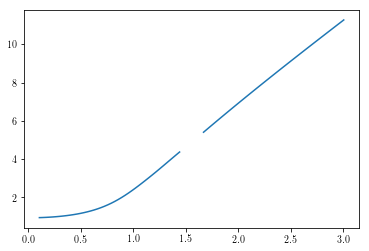
A simple solution is to change the starting guess to be away from the solution and see if it finds another one. Indeed that happens.
In [29]:
omega = sp.linspace(0.1,3,90)+1/200
amp = sp.zeros_like(omega)
x = sp.array([[0,-1,1]])
for i, freq in enumerate(omega):
#print(i,freq,x)
#print(sp.average(x))
x = x-sp.average(x)
try:
t, x, e, amps, phases = ms.hb_time(duff_osc2, x, freq, num_harmonics=4, verbose = False, f_tol = 1e-6)#, callback = resid)
amp[i]=amps[0]
except:
amp[i] = sp.nan
plt.plot(omega, amp)
Out[29]:
[<matplotlib.lines.Line2D at 0x10d766d68>]
In [30]:
omegal = sp.arange(3,.03,-1/200)+1/200
ampl = sp.zeros_like(omegal)
x = sp.array([[0,-1,1]])
for i, freq in enumerate(omegal):
# Here we try to obtain solutions, but if they don't work,
# we ignore them by inserting `np.nan` values.
x = x-sp.average(x)
try:
t, x, e, amps, phases = ms.hb_time(duff_osc2, x, freq, num_harmonics=4, f_tol = 1e-6)#, callback = resid)
ampl[i]=amps[0]
except:
ampl[i] = sp.nan
plt.plot(omegal, ampl)
Out[30]:
[<matplotlib.lines.Line2D at 0x10d581278>]
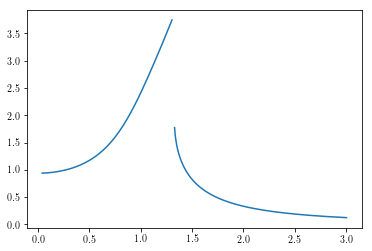
In [31]:
plt.plot(omegal,ampl)
plt.plot(omega,amp)
#plt.axis([0,3, 0, 10.5])
Out[31]:
[<matplotlib.lines.Line2D at 0x10d6ba208>]
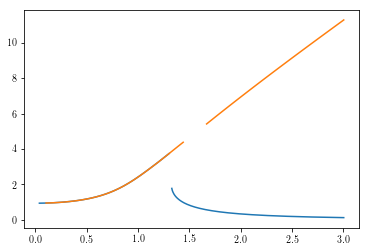
In [32]:
from scipy.optimize import newton_krylov
In [33]:
def duff_amp_resid(a):
return (mu**2+(sigma-3/8*alpha/omega_0*a**2)**2)*a**2-(k**2)/4/omega_0**2
In [34]:
mu = 0.05 # damping
k = 1 # excitation amplitude
sigma = -0.9 #detuning
omega_0 = 1 # driving frequency
alpha = 0.1 # cubic coefficient
In [35]:
newton_krylov(duff_amp_resid,-.1)
Out[35]:
array(-0.5478691201747141)
In [36]:
sigmas = sp.linspace(-1,3,200)
amplitudes = sp.zeros_like(sigmas)
x = newton_krylov(duff_amp_resid,1)
for i, sigma in enumerate(sigmas):
try:
amplitudes[i] = newton_krylov(duff_amp_resid,x)
x = amplitudes[i]
except:
amplitudes[i] = newton_krylov(duff_amp_resid,0)
x = amplitudes[i]
plt.plot(sigmas,amplitudes)
Out[36]:
[<matplotlib.lines.Line2D at 0x10da1e2e8>]
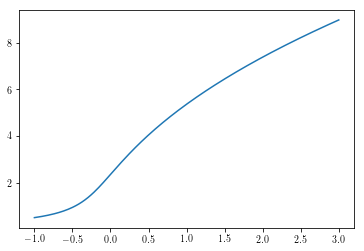
In [37]:
sigmas = sp.linspace(-1,3,200)
sigmasr = sigmas[::-1]
amplitudesr = sp.zeros_like(sigmas)
x = newton_krylov(duff_amp_resid,3)
for i, sigma in enumerate(sigmasr):
try:
amplitudesr[i] = newton_krylov(duff_amp_resid,x)
x = amplitudesr[i]
except:
amplitudesr[i] = sp.nan#newton_krylov(duff_amp_resid,0)
x = amplitudesr[i]
plt.plot(sigmasr,amplitudesr)
/Users/jslater/anaconda/lib/python3.6/site-packages/scipy/optimize/nonlin.py:474: RuntimeWarning: invalid value encountered in double_scalars
and dx_norm/self.x_rtol <= x_norm))
Out[37]:
[<matplotlib.lines.Line2D at 0x10dbea828>]
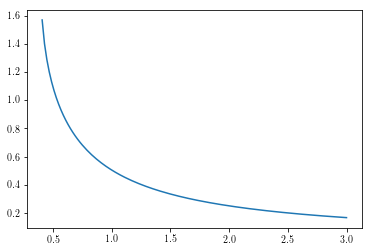
In [38]:
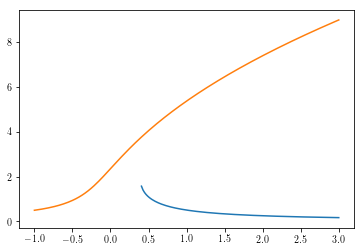
plt.plot(sigmasr,amplitudesr)
plt.plot(sigmas,amplitudes)
Out[38]:
[<matplotlib.lines.Line2D at 0x10d862160>]
Using lambda functions¶
As an aside, we can use a lambda function to solve a simple equation without much hassle. For example, \(\ddot{x} + 0.1\dot{x}+ x + 0.1 x^3 = \sin(0.7t)\)
In [14]:
def duff_osc2(x, v, params):
omega = params['omega']
t = params['cur_time']
return np.array([[-x-.1*x**3-.1*v+1*sin(omega*t)]])
_,_,_,a,_ = ms.hb_time(duff_osc2, sp.array([[0,1,-1]]), 0.7, num_harmonics=1)
print(a)
[ 1.47796291]
In [20]:
_,_,_,a,_ = ms.hb_time(lambda x,v, params:np.array([[-x-.1*x**3-.1*v+1*sin(0.7*params['cur_time'])]]), sp.array([[0,1,-1]]), .7, num_harmonics=1)
a
Out[20]:
array([ 1.47796291])
Two things to note: 1. Remember that the lambda function has to return
an n by 1 array. 2. Time must be referenced as params[‘cur_time’]